Spatial AI: Augmenting SLAM technology with deep learning
SLAM is being gradually developed towards Spatial AI, the common sense spatial reasoning which will enable robots and other artificial devices to operate in general ways in their environments-- not just localising and building geometric maps, but interacting intelligently with scenes and objects.
In the context of Spatial AI, deep learning has most obviously had a big impact on bringing semantic meaning to geometric maps of the world.

Spatial AI Brain
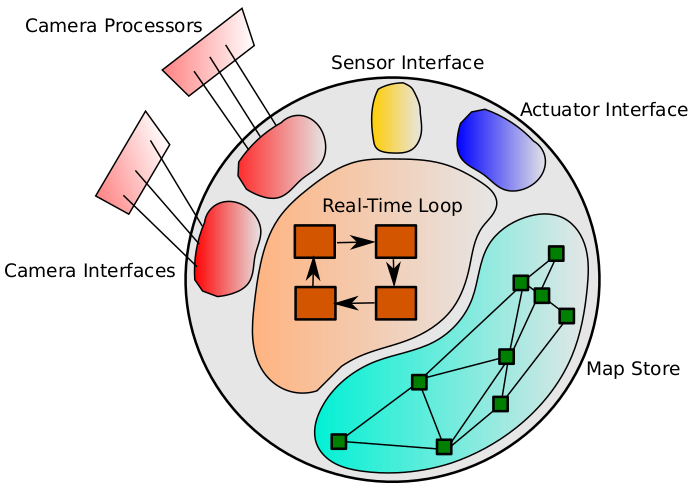
From SLAM to Spatial AI
References
- https://blog.slamcore.com/spatial-ai-slam-deep-learning
- FutureMapping: The Computational Structure of Spatial AI Systems